Друзья, этот пост я хочу начать с того, что поздравить вас с Днем Победы! Я уже рассказывал вам о том, что мой двоюродный дед пропал без вести на войне. Он приписал себе один год и пошел на фронт, оставив дома трех малолетних сестер. Эшелон, в котором он направлялся на фронт, попал под бомбежку. Мои поиски в архивах, к сожалению, ничего не дали. Вечная ему слава!
Ну, а мы с вами продолжаем изучать расчет численности персонала с помощью корреляционно-регрессионный анализа. Сегодня рассмотрим следующие два этапа.
1. Определение совокупности факторов, влияющих на численность персонала выбранного подразделения
Выбрали подразделение? Теперь нам важно набрать факторы, которые влияют на численность. Факторы выбираются просто. Создается экспертная группа, из числа самих сотрудников, их руководителей, просто экспертов, хорошо владеющих информацией о выполняемом функционале. Группа формирует перечень факторов, учитывая при этом должностные инструкции, положения о подразделениях, различные регламенты, процедуры и т.д., в которых обозначены задачи и функции исследуемого подразделения. Факторы необходимо выражать в конкретных измеримых единицах (бублики, рогалики, детали, отчеты, заявки и т.д.).
Как я уже говорил, при выборе факторов, важно учитывать наличие статистики за отчетный период по каждому. Если статистики нет, соответственно, нет и расчета. Значит, такие факторы не включаются. Выбираем другие. На данном этапе общее количество факторов ничем не ограничено. Есть экспертиза, что данный фактор влияет на численность, смело включаем его в матрицу. Позже все лишнее отпадет.
Результатом данного этапа будет таблица с исходными данными.
Таблица 1. Матрица исходных данных исследуемой функции
| № п/п | Наименование подразделения | Численность подразделения | Наименование влияющих факторов | ||||
Фактор 1 |
Фактор 2 |
Фактор 3 |
Фактор .. |
Фактор m |
|||
| 1 | Филиал 1 | ||||||
| 2 | Филиал 2 | ||||||
| 3 | Филиал 3 | ||||||
| 4 | Филиал 4 | ||||||
| 5 | Филиал 5 | ||||||
| 6 | Филиал 6 | ||||||
| … | Филиал … | ||||||
| n | Филиал n | ||||||
где n – размер выборочной совокупности; m – число факторов, влияющих на численность.
2. Сбор и определение пригодности исходных данных для применения корреляционно-регрессионного метода
Собираем статистику по каждому фактору (выборка). Определенного ограничения на размер выборки нет, но рекомендуется, чтобы она превышала число факторов, влияющих на численность, в 10 раз. Также не забываем про численность персонала каждого подразделения попавшего в исследования. Данные должны быть за определенный период, в смысле за один и тот же период по всем подразделениям.
Результат данного этапа показан в таблице 2.
Таблица 2. Заполненная матрица исходных данных исследуемой функции
| № п/п | Наименование подразделения | Численность подразделения | Наименование влияющих факторов | ||||
Фактор 1 |
Фактор 2 |
Фактор 3 |
Фактор .. |
Фактор m |
|||
| 1 | Филиал 1 | Y1 | X11 | X21 | X31 | … | Xm1 |
| 2 | Филиал 2 | Y2 | X12 | X22 | X32 | … | Xm2 |
| 3 | Филиал 3 | Y3 | X13 | X23 | X33 | … | Xm3 |
| 4 | Филиал 4 | Y4 | X14 | X24 | X34 | … | Xm4 |
| 5 | Филиал 5 | Y5 | X15 | X25 | X35 | … | Xm5 |
| 6 | Филиал 6 | Y6 | X16 | X26 | X36 | … | Xm6 |
| … | Филиал … | Y… | X1… | X2… | X3… | … | X… |
| n | Филиал n | Yn | X1n | X2n | X3n | … | Xmn |
Вот теперь с чистой совестью, мы приступаем непосредственно к математике. Для проверки условия применимости данной выборки сначала нам нужно проверить однородность этой выборки. Однородность выборки означает, что все ее элементы подчинены одной математической модели/закону. Если же для описания выборки требуются несколько моделей, то выборка неоднородна. Это из области высшей математики, раздел статистика. Если вам будет интересно, рекомендую прочесть на досуге. Увлекает, знаете ли! 🙂
Для проверки однородности выборки нам необходимо для каждого фактора рассчитать коэффициент вариации. Формула коэффициента вариации приведена ниже:
— среднеквадратичное отклонение по выборочной совокупности,
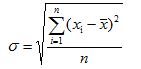
— среднее арифметическое по выборочной совокупности.
По полученному значению Vs, делается вывод об однородности совокупности исходных данных:
— совокупность однородна.
— совокупность неоднородна.
В случае если выборка неоднородна, необходимо исключить из выборки, данные с максимальным отклонением от среднего арифметического. Т.е. если вы считаете, что какой-то показатель какого-то фактора необходимо исключить из выборки, то удалить нужно всю строку.
Все расчеты рекомендую выполнять с помощью Excel. Удобная программа для таких расчетов. Набор встроенных функций помогает решать практически любую задачу.
От себя добавлю, что данную итерацию провожу редко, поскольку найти такое количество данных для выборки очень и очень проблематично. С фиксацией результатов работы у нас очень тяжело, и очень часто полученные данные пишутся тут же «с неба».
Следующим шагом будет расчет коэффициента корреляции по каждому фактору. Что же нам даст коэффициент корреляции? Коэффициент корреляции покажет нам взаимосвязь между численностью персонала и, собственно, выбранным фактором. Другими словами, изменение выбранного фактора приведет к изменению численности. Не возьмусь объяснять более подробно, поскольку все давно забыл, да и разговор у нас с вами не про математику, а про расчет численности персонала.
Расчет коэффициента корреляции необходимо также провести по каждому фактору по отношению к численности. Я рассчитываю его с помощью функции «КОРРЕЛ» в Excel. В явном виде формула расчета коэффициента корреляции выглядит следующим образом:
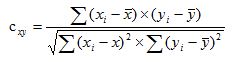
где Xi— значения переменной X;
yi— значения переменной Y;
— среднее арифметическое для переменной X;
— среднее арифметическое для переменной Y.
Теперь мы должны определить есть ли связь между фактором и численностью или нет. Для удобства интерпретации коэффициента, можно применять вот такую таблицу:
Таблица 3. Интерпретация коэффициента корреляции
| Диапазон значений коэффициента корреляции | Характер связи |
| |1| | Функциональная |
| -1 < Cij < -0,7 | Обратная сильная |
| -0,7 < Cij < -0,5 | Обратная умеренная |
| -0,5 < Cij < 0 | Обратная слабая |
| 0 | Связь отсутствует |
| 0 < Cij < 0,5 | Прямая слабая |
| 0,5 < Cij < 0,7 | Прямая умеренная |
| 0,7 < Cij < 1 | Прямая сильная |
И вот здесь как раз включается связь с предыдущим этапом – определение причинно-следственной связи между численностью и факторами. Здесь как раз и может скрываться самая большая ошибка. Дело в том, что когда к определению факторов привлекаешь экспертов со стороны подразделений, непосредственно выполняющих исследуемую функцию, то, как правило, они начинают включать в матрицу все мыслимые и немыслимые факторы. Конечно, большая часть из них отбрасывается на этапе получения статистики, но некоторые остаются. И если вдруг, один из них покажет высокий коэффициент корреляции, а это означает, что связь существует и данный фактор подлежит включению в модель. Но! Здравый смысл вам подсказывает, что эта связь случайна и никакими аргументами объяснить эту связь невозможно. Как поступать в этом случае? Все просто! Исключайте этот аргумент из выборки. Если же эксперты настаивают, то можно запросить у них дополнительную статистику за другие периоды и провести корреляционный анализ на новых данных. Уверен, что скачки коэффициента корреляции будут очень большими. Вот вам и аргумент для исключения!
Хочу еще раз обратить ваше внимание на объем выборки. Брать статистику за период, когда в подразделениях происходили какие-либо изменения нет смысла. Лучше если это период будет относительно спокойным. Без всяких новшеств и оптимизаций. Ну и конечно, период лучше брать большой.
После того, как мы получили коэффициенты корреляции по каждому фактору, нам необходимо провести анализ на предмет выявления факторов линейно зависимых друг от друга. Приведу пример. Во время исследований в матрицу факторов попали несколько факторов, один из которых являлся суммой двух или нескольких факторов, также вошедших в матрицу исходных данных. Вроде бы такие случаи должны отсеиваться сразу на этапе экспертизы, но это только в идеале. На практике, я очень часто сталкиваюсь с тем, что в матрицу исходных данных попадают, в том числе, и производные от какого-то основного фактора.
Но, в тоже время, здесь работает все тот же здравый смысл. Если у вас коэффициент корреляции высок, но вы уверены, что они независимы друг от друга, то в качестве проверки возьмите дополнительную выборку данных. Если связь снижается, то оставляем, если же увеличивается или постоянна, то однозначно исключаем.
Все результаты сравнения факторов между собой удобно показывать в корреляционной матрице.
| № п/п | Наименование влияющих факторов | Наименование влияющих факторов | |||||
Фактор 1 |
Фактор 2 |
Фактор 3 |
Фактор 4 |
Фактор… |
Фактор m |
||
| 1 | Фактор 1 | 1,0 | |||||
| 2 | Фактор 2 | C12 | 1,0 | ||||
| 3 | Фактор 3 | C13 | C23 | 1,0 | |||
| 4 | Фактор 4 | C14 | C24 | C34 | 1,0 | ||
| … | Фактор … | C1.. | C2… | C3… | C4… | 1,0 | |
| n | Фактор m | C1m | C2m | C3m | C4m | C…m | 1,0 |
Выбираем из таблицы пары факторов, коэффициент корреляции, которых превышает 0,7. Этот коэффициент называется парный коэффициент корреляции. Начинаем анализировать каждую пару факторов. Один из них мы должны исключить. Смотрим, какой из пары фактор имеет наиболее высокую корреляцию с нашей численностью. Оставляем! Если один из коэффициентов входит в несколько пар, но оказывает наиболее высокой влияние на численность, однозначно его оставляем, а оставшиеся исключаем из нашей матрицы.
В итоге у нас с вами должна получиться матрица из нескольких факторов, имеющих максимальные коэффициенты корреляции и, собственно, сама численность. Для удобства представление информации вы можете сделать таблицу и парами факторов, в которой один из столбцов будет показывать коэффициент корреляции каждого фактора на численность в отдельности.
Теперь переходит к самому приятному – непосредственному построению математической модели расчета численности персонала.
3. Построение регрессионной модели.
Регрессионная модель линейной корреляции в общем виде имеет следующий вид:
– теоретическое значение численности при X1, X2, …Xm — определенных значениях факторов, влияющих на нее.
а1,а2…аm- коэффициенты множественной регрессии
b – свободный член уравнения.
Сама модель регрессии делается с помощью метода наименьших квадратов основанного на минимизации суммы квадратов отклонений некоторых функций от искомых переменных. Я не берусь рассказывать вам про этот метод, поскольку наверняка многие из вас «заткнут меня за пояс» в части математической статистики, да и направление у нас нормирование, а не математика. Я получаю модель с помощью Excel, точнее с помощью встроенной функции ЛИНЕЙН. При выборе данной функции у вас открывается диалоговое окно, в котором вы должны ввести известные значения Y (это наша с вами численность), в следующей строке известные значения X (это значения факторов), ввести константу (1 или 0), ввести показатель статистики (1 или 0), и нажать ОК. Далее, по рекомендации Excel, вам необходимо выполнить несложную итерацию ввода данных как массива (выделить необходимые ячейки, потом нажать клавишу F2, а затем — клавиши CTRL + SHIFT + ВВОД). Все подробности выполнения применения данной функции вы можете получить из справки Excel.
В итоге вы получаете набор коэффициентов (ровно по количеству факторов), свободный член (если его потребность вы задавали) и… Ву-а-ля! Формула расчета численности персонала в зависимости от факторов у вас есть!
Друзья, я намеренно не стал рассказывать вам про коэффициенты детерминации, F-статистику и Т-статистику, стандартную ошибку уравнения регрессии. Считаю, что в случае расчета нормативной численности этими данными можно пренебречь (хотя сам применяю достаточно часто). Просто, в двух словах это не расскажешь, а скомкать – вам будет не понятно. Поэтому, прошу не судить меня строго и отнестись ко мне благосклонно. Моя задача состоит в том, что показать вам, как можно применить математические методы в нормировании труда, какой будет результат и, самое главное, что сделать это совсем не тяжело. Данный метод активно применялся в Советском Союзе при нормировании численности ИТР (инженерно-технический персонал). Я как-то раз обучался у одного из старейших специалистов по нормированию труда, и он рассказывал нам про все тонкости этого метода. Сейчас я достаточно активно пользуюсь им. Результат впечатляет!
В заключении теоритической части добавлю еще одно ограничение данного метода. С помощью корреляционно-регрессионного анализа мы с вами получим нормы численности. Если дальше развивать модель, то из нее мы получить нормы выработки. И, в принципе, с учетом классической теории нормирования труда, где норма выработки прямо пропорциональна норме времени (хотя я с этим утверждением не согласен), можно получить и норму времени. Но! Модель построенная с помощью регрессии не учитывает внутреннее распределение затрат рабочего времени, строится на основе фактически сложившихся трудовых и производственных процессов и, в случае, изменения этих самых процессов подлежит пересмотру. Другими словами, при значительном изменении внутренних процессов, нам с вами придется выполнять все этапы заново, не забывая дать этим процессам устоятся, а сотрудникам привыкнуть. Мы не сможет взять элементы уравнения и построить нормальный баланс сотрудников или рассчитать новую норму. Нет! Начиная с первого этапа, мы должны пройти их все, ничего не пропуская.
Приветствую.
Отлично, даже добавить нечего)
Вячеслав, добрый день!
Спасибо за оценку! Хотя мне несколько жаль отсутствие критики! Вы спец в нашем деле, поэтому ваши замечания и комментарии для меня важны.
Добрый день!
Давно использую такой метод, но чтобы ттак его изложить в тексте — выше всяких похвал!!!
Антон, спасибо!
Давненько не общались! Как успехи в банковском секторе?
Александр, искрене рад за твой сайт. Извини не часто захожу, но иногда обращаюсь — «А, ну-ка, как там у Александа написано?»))).
Озадачился расчетом норм управляемости. Понятно, что есть рекомендации МинТруда и в каждой отрасли, да и в каждом подразделении норма управляемости будет своя, но хочется унифицированных инструмент. Есть мысли, но они «скрипят» о бумагу — не ложатся. Может поможешь?
Антон, привет! Ну у тебя вопросы, как всегда, непростые! 🙂
Реально расчета норм управляемости я нигде не встречал. Вернее вразумительного расчета.
Единственно, что мне понравилось, я читал у Пригожина А.И. «Методы развития организаций».
У нас мы поступили просто: определили минимальную численность в зависимости от уровня подразделения и установили потолок численности свыше которой вводится заместитель подразделения. Этот потолок был разным для методологических и операционных подразделений. И все это было получено эмпирическим путем, т.е. «из жизни».
Утвердили! Вроде работает!